- We will now apply Ampere circuital law to calculate magnetic field of a toriod
- A toriodal solenoid is a hollow circular ring with a large number of turns of a wire carrying current wound around the ring
- Suppose we have to find the magnetic field B at a point P inside the toriod as shown below in figure
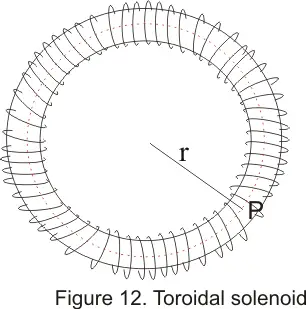
- In this case amperion loop would be a circle through point P and concentric inside the toriod
- By symmetry field will have equal magnitude at all points of this circle and this field is tangential to every point in the circle
Thus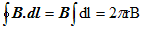
- If there are total N number of turns ,net current crossing the area bounded by the circle is NI where I is the current in the toriod
- using Ampere law
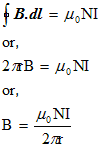
Thus we see that field B varies with r i.e. field B is not uniform over the cross-section of the core because the path l=2πr is longer at the outer side of the section then at the inner side - Imagine a concentric circle through point P' outside the toriod
- The net current passing through this circular disc is zero ,since the current NI passes in and same current passes out. Thus using Ampere's circuital law, the field B=0 outside the torriod


 0
0

