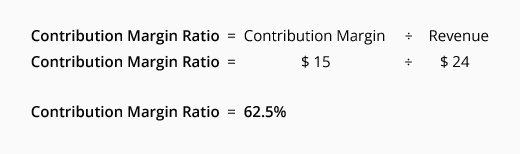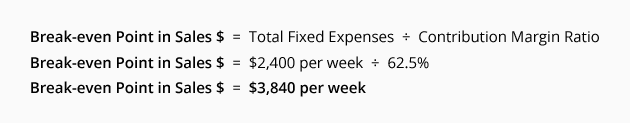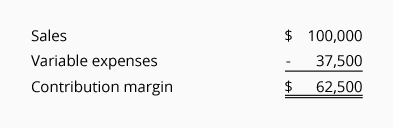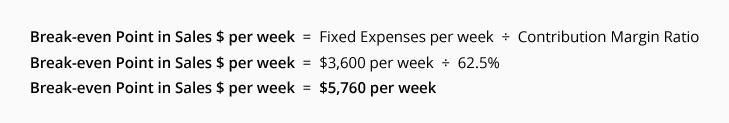i. Break Even Point: The break–even point (BEP) or break–evenlevel represents the sales amount in either unit (quantity) or revenue (sales) terms that is required to cover total costs, consisting of both fixed and variable costs to the company. Total profit at the break-even point is zero.
ii. Expense Behavior: At the heart of break-even point or break-even analysis is the relationship between expenses and revenues. It is critical to know how expenses will change as sales increase or decrease. Some expenses will increase as sales increase, whereas some expenses will not change as sales increase or decrease.
a. Variable Expenses: Variable expenses increase when sales increase. They also decrease when sales decrease.
At Oil Change Co. the following items have been identified as variable expenses. Next to each item is the variable expense per car or per oil change:
The other expenses at Oil Change Co. (rent, heat, etc.) will not increase when an additional car is serviced.
For the reasons shown in the above list, Oil Change Co.’s variable expenses will be $9 if it services one car, $18 if it services two cars, $90 if it services 10 cars, $900 if it services 100 cars, etc.
b. Fixed Expenses: Fixed expenses do not increase when sales increase. Fixed expenses do not decrease when sales decrease. In other words, fixed expenses such as rent will not change when sales increase or decrease.
At Oil Change Co. the following items have been identified as fixed expenses. The amount shown is the fixed expense per week:
c. Mixed Expenses: Some expenses are part variable and part fixed. These are often referred to as mixed or semi-variable expenses. An example would be a salesperson’s compensation that is composed of a salary portion (fixed expense) and a commission portion (variable expense). Mixed expenses could be split into two parts. The variable portion can be listed with other variable expenses and the fixed portion can be included with the other fixed expenses.
iii. Revenues or Sales: Revenues (or sales) at Oil Change Co. are the amounts earned from servicing cars. Oil Change Co. charges one flat fee of $24 for performing the oil change service. For $24 the company changes the oil and filter, adds needed fluids, adds air to the tires, and inspects engine belts.
At the present time no other service is provided and the $24 fee is the same for all automobiles regardless of engine size.
As the result of its pricing, if Oil Change Co. services 10 cars its revenues (or sales) are $240. If it services 100 cars, its revenues will be $2,400.

iv. Desired Profit In Units Let’s say that the owner of Oil Change Co. needs to earn a profit of $1,200 per week rather than merely breaking even. You can consider the owner’s required profit of $1,200 per week as another fixed expense. In other words the fixed expenses will now be $3,600 per week (the $2,400 listed earlier plus the required $1,200 for the owner). The new point needed to earn $1,200 per week is shown by the following break-even formula:
Always check your calculations:
The above schedule confirms that servicing 240 cars during a week will result in the required $1,200 profit for the week.
v. Break-even Point In Sales Dollars: One can determine the break-even point in sales dollars (instead of units) by dividing the company’s total fixed expenses by the contribution margin ratio.
The contribution margin ratio is the contribution margin divided by sales (revenues). The ratio can be calculated using company totals or per unit amounts. We will compute the contribution margin ratio for the Oil Change Co. by using its per unit amounts:
The break-even point in sales dollars for Oil Change Co. is:
The break-even point of $3,840 of sales per week can be verified by referring back to the break-even point in units. Recall there were 160 units necessary to break-even. At $24 per unit the necessary sales in dollars would be $3,840.
vi. Desired Profit In Sales Dollars: Let’s assume a company needs to cover $2,400 of fixed expenses each week plus earn $1,200 of profit each week. In essence the company needs to cover the equivalent of $3,600 of fixed expenses each week.
Presently the company has annual sales of $100,000 and its variable expenses amount to $37,500 per year. These two facts result in a contribution margin ratio of 62.5%:
The amount of sales necessary to give the owner a profit of $1,200 per week is determined by this break-even point formula:
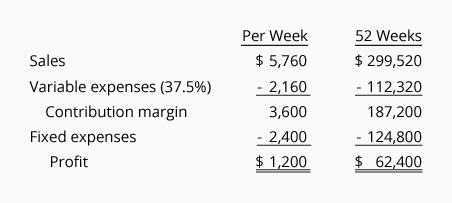
To verify that this answer is reasonable, we prepared the following schedule:
As you can see, for the owner to have a profit of $1,200 per week or $62,400 per year, the company’s annual sales must triple. Presently the annual sales are $100,000 but the sales need to be $299,520 per year in order for the annual profit to be $62,400.


 0
0