Find the best tutors and institutes for Class 10 Tuition
Search in
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Let a be any positive integer and b = 6. Then, by Euclid’s algorithm,
a = 6q + rfor some integer q ≥ 0, and r = 0, 1, 2, 3, 4, 5 because 0 ≤ r < 6.
Therefore, a = 6q or 6q + 1 or 6q + 2 or 6q + 3 or 6q + 4 or 6q + 5
Also, 6q + 1 = 2 × 3q + 1 = 2k1 + 1, where k1 is a positive integer
6q + 3 = (6q + 2) + 1 = 2 (3q + 1) + 1 = 2k2 + 1, where k2 is an integer
6q + 5 = (6q + 4) + 1 = 2 (3q + 2) + 1 = 2k3 + 1, where k3 is an integer
Clearly, 6q + 1, 6q + 3, 6q + 5 are of the form 2k + 1, where k is an integer.
Therefore, 6q + 1, 6q + 3, 6q + 5 are not exactly divisible by 2. Hence, these expressions of numbers are odd numbers.
And therefore, any odd integer can be expressed in the form 6q + 1, or 6q + 3,
or 6q + 5
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Maximum number of columns in which the Army contingent and the band can march = HCF (616, 32)
Appplying Euclid's algorithm to find the HCF.
Step 1: since 616 > 32 so applying Euclid's division lemma to a= 616 and b= 32 we get integers q and r as 32 and 19
i.e 616 = 32 x 19 + 8
Step 2: since remainder r =8 
0 so again applying Euclid's lemma to 32 and 8 we get integers 4 and 0 as the quotient and remainder
i.e 32 = 8 x 4 + 0
Step 3: Since remainder is zero so divisor at this stage will be the HCF
The HCF (616, 32) is 8.
Therefore, they can march in 8 columns each.
Use Euclid's division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m. [Hint : Let x be any positive integer then it is of the form 3q, 3q + 1 or 3q + 2. Now square each of these and show that they can be rewritten in the form 3m or 3m + 1.]
Let 'a' be any positive integer we need to prove that a2 is of the form 3m or 3m + 1 for some integer m.
Let 'b' = 3 be the other integer
Applying Euclid's division lemma to a and b=3
We get a = 3q + r for some integer q 
0and r = 0, 1, 2
Therefore, a = 3q or 3q + 1 or 3q + 2
Now Consider a2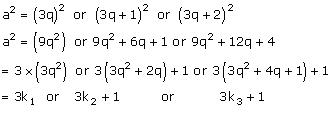
Where k1 = 3q2, k2 =3q2+2q and k3 = 3q2+4q+1 since q ,2,3,1 etc are all integers so is their sum and product.
So k1 k2 k3 are all integers.
Hence, it can be said that the square of any positive integer is in the form 3m or 3m + 1 for any integer m.
Use Euclid's division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Let a be any positive integer and b = 3
By applying Euclid's division algorithm,
a = 3q + r, where q 
0 and 0
r < 3
Case 1: When a = 3q,
Therefore, every number can be represented as these three forms. There are three cases.
Use Euclid's division algorithm to find the HCF of : (i) 135 and 225 (ii) 196 and 38220 (iii) 867 and 255
(i) 135 and 225
apply Euclid's division lemma
225 = 135 x 1 + 90
The HCF of 135 and 225 is 45.
135 = 90 x 1 + 45
90 = 2 x 45 + 0
Therefore, HCF of 135 and 225 is 45.
(ii) 196 and 38220
apply Euclid's division lemma
38220 = 196 x 195 + 0
Therefore, HCF of 196 and 38220 is 196.
(iii) 867 and 255
apply Euclid's division lemma,
867 = 255 x 3 + 102
255 = 102 x 2 + 51
102 = 51 x 2 + 0
Therefore, HCF of 867 and 255 is 51.
How helpful was it?
How can we Improve it?
Please tell us how it changed your life *
Please enter your feedback
UrbanPro.com helps you to connect with the best Class 10 Tuition in India. Post Your Requirement today and get connected.
Find best tutors for Class 10 Tuition Classes by posting a requirement.
Get started now, by booking a Free Demo Class
